ESCUELA SUPERIOR DE ADMINISTRACIÓN PÚBLICA ESAP TERRITORIAL CAUCA
ESTUDIANTES DE IV. SEMESTRE DE APT. CETAP POPAYÁN
Esp. Fabiàn Orozco M.
Tutor.
Número índice : Aquella medida estadística que sirve para comparar una magnitud ( o un conjunto de magnitudes) en dos situaciones (temporales o espaciales ) distintas; una de las cuales se considera como referencia. (Normalmente se tratará de comparar períodos de tiempo distintos)
Período base o referencia: Será la situación inicial o el periodo tomado como referencia.(subíndice 0)
Período actual: la situación que quiere comparase.(subíndice t)
Clasificación: Los números índices pueden ser:
SIMPLES: pretenden hacer comparaciones sobre una sola magnitud simple.(p.ej. el precio del trigo). Habitualmente se definen como ratios (razón) entre el valor actual y el valor del período base.
para la magnitud simple Xi
COMPLEJOS: pretenden hacer comparaciones sobre una magnitud compleja, consistente en la agregación de varias magnitudes simples.(p.ej. precio de los cereales,cotización bursátil de un grupo (químicas,p.ej.).Habitualmente se utilizan promedios de índices simples (media aritmética, geométrica, armónica o agregativa).
Complejos SIN PONDERAR: Se utiliza un promedio de índices simples de cada magnitud simple Xi , sin ponderarlos: (dado un agregado de magnitudes X1,X2,X3,...,XI.)
media aritmética: 
media agregativa:

En menor medida se usan también las medias geométricas y armónica.
Complejos PONDERADOS : se utiliza un promedio de índices simples de cada magnitud, Xi , ponderado cada uno de ellos por un peso wi , distinto en cada caso.
media aritmética ponderada:

media agregativa ponderada:

Números índices simples (precios, cantidades y valor ):
Simplemente se trata de relativizar los precios, las cantidades o los valores respecto del año base.
Ejemplo: sean las siguientes cifras de producción y precios de ARROZ
y los correspondientes índices simples de precios (
| PERIODO | PRECIO | CANTIDAD | VALOR | ÍNDICEPRECIOS (PREC.REL.) | ÍNDICE CANTIDADES(CANT.REL.) | ÍNDICE VALORES(VAL.REL.) |
0
|
50
|
10
|
500
|
1
|
1
|
1
|
1
|
60
|
15
|
900
|
1,2
|
1,5
|
1,8
|
2
|
70
|
20
|
1400
|
1,4
|
2
|
2,8
|
3
|
75
|
30
|
2250
|
1,5
|
3
|
4,5
|
4
|
80
|
40
|
3200
|
1,6
|
4
|
6,4
|
5
|
90
|
50
|
4500
|
1,8
|
5
|
9
|
Números índices de precios.
Son números índices evaluados para magnitudes precios.
Índices de precios no ponderados: Dado un conjunto de artículos:
Índice de Sauerbeck: de precios es la media aritmética de los índices simples (de precios) de cada artículo:
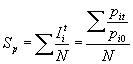
Índice de Bradstreet-Dûtot : es la media agregativa de los precios: 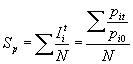
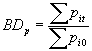
Ejemplo: Obtener los índices de precios de Sauerbeck y de Bradstreet-Dûtot para el conjunto de productos agrícolas : Arroz, trigo y patatas:
| Arroz | Trigo | Patatas | Arroz | Trigo | Patatas | I.Sauerbeck | I.B-Dûtot | |
| Periodo | Precio | Precio | Precio | I.Simple | I.Simple | I.Simple | (M-aritm.) | (M.agreg.) |
0
|
50
|
30
|
40
|
1
|
1
|
1
|
1
|
1
|
1
|
60
|
30
|
40
|
1,2
|
1
|
1
|
1,06666666
|
1,08333333
|
2
|
70
|
35
|
45
|
1,4
|
1,1666
|
1,125
|
1,23055555
|
1,25
|
3
|
75
|
40
|
45
|
1,5
|
1,3333
|
1,125
|
1,31944444
|
1,33333333
|
4
|
80
|
45
|
50
|
1,6
|
1,5
|
1,25
|
1,45
|
1,45833333
|
5
|
90
|
50
|
50
|
1,8
|
1,6666
|
1,25
|
1,57222222
|
1,58333333
|
Dependiendo de las ponderaciones para cada bien (o articulo) y del tipo de promedio que se utilice se podrán generar distintos índices:
Índice de Laspeyres : Es la media aritmética ponderada de los índices simples de cada articulo utilizándose como ponderación para cada bien: wi = pi0.qi0 , esto es la ponderación para cada artículo será el valor de la cantidad consumida o vendida o producida del bien i-simo en el período base al precio del período base.
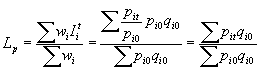
Índice de Pasche: Es la media aritmética ponderada de los índices simples de cada articulo utilizándose como ponderación para cada bien: wi=pi0.qit , esto es,el valor a precio del período base de la cantidad consumida en el período actual.
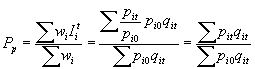
Índice de Fisher: Es simplemente la media geométrica de los dos anteriores.
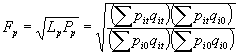
Índice de Edgeworth: Es la media agregativa ponderada de los índices simples de precios de cada artículo, utilizando como ponderación wi=qi0+qit Es decir, la suma de las cantidades consumidas, producidas o vendidas de cada artículo en el año baso y en el corriente :
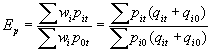
Ejemplo números índices ponderados

1. Existencia. Todo número índice ha de existir: Ha de tener un valor finito distinto de cero.Cumplimiento de las propiedades por los índices de precios.
2. Identidad.Si se hacen coincidir el período base y el período actual el número índice debe ser 1.
3. Inversión.Si se intercambian el período base y el período actual los índices deben ser los valores recíprocos:
It0 = 1/ I0t
4. Proporcionalidad.Si en el período actual todas las magnitudes sufren una variación proporcional, el número índice debe variar afectado por esta proporcionalidad.
5. Homogeneidad. Un número índice no debe quedar afectado por un cambio en las unidades de medida.
1. Existencia. La cumplen los seis.
2. Identidad.La cumplen los seis.
3. Inversión.Sólo la verifican los índices de Bradstreet-Dûtot, Edgeworth y Fisher.
4. Proporcionalidad.La satisfacen los seis, pero los resultados de una transformación proporcional son anómalos desde el punto de vista económico en el caso de los índices de Paasche, Edgeworth y Fisher, pues suponer que al variar los precios las cantidades se mantengan siempre constantes, es algo excesivo.
5. Homogeneidad.No la cumple ninguno.
En resumen: el índice de Bradstreet-Dûtot es el que más propiedades cumple, pero es un índice no ponderado, por lo que se suele preferir el índice de Laspeyres que es el único índice ponderado que cumple la proporcionalidad sin producir contrasentidos económicos.
Deflactación de series estadísticas
Si disponemos de una serie estadística de datos sobre la valoración de alguna magnitud económica (consumo , producción,
etc ), lo habitual es que la valoración monetaria de estos datos se realice a precios corrientes de cada período.En la medida en que los precios sufren alteraciones de unos períodos a otros, la serie así representada no permite hacer comparaciones.La solución de este problema es expresar la serie en términos de precios constantes de un determinado período (año base).
Es decir realizar la transformación:etc ), lo habitual es que la valoración monetaria de estos datos se realice a precios corrientes de cada período.En la medida en que los precios sufren alteraciones de unos períodos a otros, la serie así representada no permite hacer comparaciones.La solución de este problema es expresar la serie en términos de precios constantes de un determinado período (año base).
| Período | Valor nominal (ptas.corrientes) | Valor real (ptas. constantes) |
| 0 | V0=S pi0.qio | V0R=S pi0.qio |
| 1 | V1=S pi1.qi1 | V1R=S pi0.qi1 |
| . | ||
| t | Vt=S pit.qit | VtR=S pi0.qit |
| . | ||
| T | VT=S piT.qiT | VTR=S pi0.qiT |
El paso de la serie original a la serie valorada en precios constantes se llama deflactación, y el índice a través del cual se puede pasar de una serie a la otra se llama deflactor.La deflactación de series es una de las utilidades importantes de los números índices.
Puede probarse que se si utiliza como deflactor el índice de precios de Laspeyres no se consigue el objetivo de obtener la valoración a precios constantes; sin embargo, si se utiliza el índice de Paasche sí se consigue cambiar la serie a valores constantes.
Cambio de base y empalme.
Otro problema que se plantea es la pérdida de representatividad de los índices al ir alejándonos del período base, especialmente cuando las ponderaciones utilizadas se refieren al período base .Este problema suele resolverse renovando cada cierto tiempo la evaluación de los índices, cambiando de período base .
Si se lleva a cabo una renovación del índice en un determinado período a partir de ese período se evaluarán los índices mediante otras ponderaciones y la serie quedará dividida en dos partes no homogéneas:
| año | índice | año base |
| 1985 | 1 (100) | 1985 |
| 1986 | 1.15 (115) | 1985 |
| 1987 | 1.25 (125) | 1985 |
| 1988 | 1.39 (139) | 1985 |
| 1989 | 1.60 (160) | 1985 |
| 1990 | 1 (100) | 1990 |
| 1991 | 1.2 (120) | 1990 |
| 1992 | 1.3(130) | 1990 |
| 1993 | 1.5 (150) | 1990 |
La homogeneización de la serie se resuelve empalmando las dos series de forma que manteniendo el índice 100 ( 1) para el nuevo año base los índices anteriores mantengan la proporcionalidad .(Regla de tres ).Para poder realizar el empalme es necesario conocer el índice del nuevo año base referido al antigua año base ( en nuestro caso el índice de 1990 referido a 1985): supongamos que es 1.90 (190), entonces la serie homogénea sería:
| año | empalme | índice |
| 1985 | 1 /1.90 =0.5263 | 0.5263 (52.63) |
| 1986 | 1.15 /1.90=0.6052 | 0.6052 (60.52) |
| 1987 | 1.25 /1.90=0.6578 | 0.6578 (65.78) |
| 1988 | 1.39 /1.90=0.7315 | 0.7315(73.15) |
| 1989 | 1.60 /1.90=0.8421 | 0.8421 (84.21) |
| 1990 | 1 (100) | |
| 1991 | 1.2 (120) | |
| 1992 | 1.3(130) | |
| 1993 | 1.5 (150) |
Indicadores relevantes: I.P.C, I.Producción Industrial,Índices Bursátiles, Índices de comercio Exterior: ver:
Escuder,R.:"Métodos estadísticos aplicados a la Economía" Ariel.
Martín-Guzman,P y M.Pliego,J: "Curso Básico de Estadística".Ed. A.C.
Martín Pliego,F.J.: "Introducción a la Estadística Económica y Empresarial ".Ed. AC.
ACTIVIDAD EN GRUPOS DE 4 ESTUDIANTES: VER Y ESTUDIAR EL SIGUIENTE VIDEO:
https://www.youtube.com/watch?v=oS75IONmljk


No hay comentarios:
Publicar un comentario