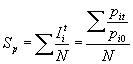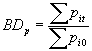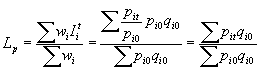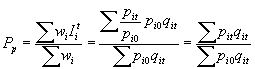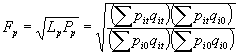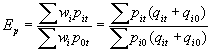Concepto y clasificación
Esp. Fabián Orozco Méndez
Tutor.
En general, las magnitudes socioeconómicas varían en el tiempo y en el espacio. Con frecuencia estaremos interesados en hacer comparaciones de dichas magnitudes en dos o más periodos de tiempo o en dos o más zonas geográficas. Por ejemplo, analizar la evolución del PIB español en los últimos años, comparar el PIB de los países europeos o, lo que es de más interés, estudiar la evolución de los precios de los productos de consumo a lo largo del tiempo o comparar el nivel de desarrollo de los países del mundo.
Un número índice, es una medida estadística que recoge la evolución relativa en el periodo t de una magnitud económica (precios, producciones, …) de un conjunto de bienes o productos respecto de un periodo base o de referencia 0. También permite comparar una magnitud económica en una zona geográfica respecto de una zona de referencia. Por tanto, permiten comparar el estado de un fenómeno económico (precios, producción,...) en dos situaciones y es una herramienta imprescindible en los estudios de coyuntura. Utilizaremos la notación de los índices temporales, cuyo uso es más habitual que los espaciales, si bien los desarrollos se pueden generalizar en gran medida a estos últimos.
- Período base o de referencia: período de tiempo fijado arbitrariamente que se toma como origen de las comparaciones.
- Período actual o corriente: período de tiempo que se compara con el período base.
Tipos de números índices
Según que recojan la evolución de una o más magnitudes:
- Índices simples: recogen la evolución del precio, la cantidad o el valor de un único bien o producto.
- Índices compuestos, complejos o sintéticos: recogen la evolución conjunta de los precios, las cantidades o los valores de kbienes o productos. A su vez, los índices complejos se clasifican como:
- Sin ponderar: todas las magnitudes o componentes tiene la misma importancia, es decir, los mismos pesos. Los k bienes o productos se consideran con el mismo peso.
- Ponderados: cada magnitud o componente tiene un peso diferente asignado en función de diversos criterios. Los kbienes o productos se consideran con distinto peso, peso que recoge la importancia relativa de cada uno de los bienes.
Simples
| |||
Números índices
|
Compuestos o complejos
|
Sin ponderar
|
Sauerbeck, Brandstreet-Dûtot, …
|
Ponderados
|
Laspeyres, Paasche, Edgeworth, Fisher, …
|
Según el tipo de magnitud:
- Índices de precios: estudian la evolución de los precios de un bien o de un conjunto de bienes.
- Índices de cantidades: estudian la evolución de la cantidad producida o consumida de un bien o de un conjunto de bienes.
- Índices de valores: estudian la evolución del valor de un bien o de un conjunto de bienes.
Precios
| |
Números índices
|
Cantidades
|
Valores
|
VENTAJAS Y APLICACIÓN DE LOS NÚMEROS ÍNDICE.
Al paso de los años los números índice han llegado a ser cada vez más importantes para la administración como indicadores de la cambiante actividad económica o de negocios; de hecho, su uso se ha convertido en el procedimiento de más amplia aceptación.
Los números índices, constituyen un sencillo artificio para comparar los términos de una o varias series cronológicas; considerando ésta última como una sucesión de observaciones de una variable tomada en instantes sucesivos.
En muchos problemas de Economía interesa combinar, mediante un promedio adecuadamente definido varios índices simples para obtener un índice con el que se trata de reflejar la evolución de una magnitud no fácil de definir concretamente, por ejemplo: coste de vida, nivel de salarios, comercio exterior, etc.
ACTIVIDAD EN GRUPOS DE 4 ESTUDIANTES:
A. En los espacios entre los párrafos, faltan las fórmulas de cada Tipo de Número Ínfice, Consúltenlas y escríbanlas, según corresponda a cada enunciado.
B. Escriban una conclusión general que resuma todo este contenido.
C. Entregar en hojas de papel cuadriculado. en la tercera tutoría de marzo de 2020
Es una medida estadística diseñada para poner de relieve cambios en una variable o en un grupo de variables relacionadas con respecto al tiempo, situación geográfica, ingreso o cualquier otra característica. Una colección de números índice para diferentes años, lugares, etc.; se llama a veces serie de índices.
Los números índices miden el tamaño o la magnitud de algún objeto en un punto determinado en el tiempo, como el porcentaje de una base o referencia en el pasado
En realidad, los números índices relacionan una o varias variables de un período dado con la misma variable o variables en otro período, llamado período base.
Los números índices se usan para hacer comparaciones. Por ejemplo, con los números índices podemos comparar los costes de alimentación o de otros servicios en una ciudad durante un año con los del año anterior, o la producción de arroz en un año en una zona del país con la otra zona. Aunque se usa principalmente en Economía e Industria; los números índices son aplicables en muchos campos. En Educación, por ejemplo, se pueden usar los números índices para comparar la inteligencia relativa de estudiantes en sitios diferentes o en años diferentes.
Muchos gobiernos se ocupan de elaborar números índice (o índices, como se les llama a veces) con el propósito de predecir condiciones económicas o industriales, tales como: índices de precios, de producción, salariales, del consumidor, poder adquisitivo, costo de vida y tantos otros.
Tal vez el más conocido sea el índice de coste de la vida o índice de precios al consumo, que prepara el Instituto de Estadística. En muchos contratos aparecen ciertas cláusulas de revisión que producen aumentos salariales automáticos correspondientes a los aumentos del índice de precios al consumo.
Las relaciones de precios es uno de los ejemplos más simple de un número índice, que no es sino el cociente entre el precio de un artículo en un período determinado y su precio en otro período, conocido como período base o período de referencia. Suponiendo que los precios en cada período son constantes. Si no lo son, podemos tomar un promedio adecuado para el período de modo que la suposición sea esencialmente válida.
La fórmula para calcular un índice de precios es la siguiente:
La relación de precios se expresa habitualmente como un porcentaje multiplicándola por 100.
En general, si Pa y Pb son los precios de un artículo durante los períodos a y b, respectivamente, la relación de precios en el período b con respecto al período a se define como Pb/Pa y se denota por Pa/b’, notación que facilita el entendimiento; con esta notación la relación de precios en la ecuación:
Ejemplo:
Supongamos que los precios pagados a pescadores por el lenguado fueron en los años 1990 y 1991 de Bs. 120 y 100 respectivamente, siendo 1990 el año base y 1991 el año dado.
Al seleccionar el período base para un índice en particular se deben observar dos reglas: Primera; el período seleccionado debe ser, en cuanto sea posible, de normalidad o estabilidad económica, no en uno que se encuentre o en el punto máximo de una economía en expansión, cerca de él, o en la cima de una recesión o economía en declinación. Así, por ejemplo, los años de la depresión de la década de 1930 no puede utilizarse como años base, ya que durante este período se produjo una reducción brusca en los precios, el año base debe ser un año en el que la actividad económica transcurra sin estas bruscas fluctuaciones. Segunda: el período base debe ser reciente, para que las comparaciones no resulten afectadas indebidamente por cambios en tecnología, calidad del producto o cambios de actitud frente al mismo, intereses, gustos y hábitos de los consumidores.
Los Pa, Pb, Pc; muestran los precios en los períodos a, b, c; respectivamente, por lo tanto los precios se asocian a un grupo de propiedades:
ü PROPIEDAD IDENTIDAD: Pa/a=1 esto dice que la relación de precios para un período respecto de él mismo es 1, es decir, 100%.
ü PROPIEDAD DE INVERSIÓN TEMPORAL: Pa/Pb/a=1. es decir, Pa/b= 1/Pb/a. Si dos períodos se intercambian, las correspondientes relaciones de precios son cada una la inversa de la otra.
ü PROPIEDAD CÍCLICA O CIRCULAR:
Pa/bPb/a=1;
Pa/bPb/cPc/a=1;
Pa/bPb/cPc/dPd/a=1;
Pa/bPb/cPc/dPd/ePe/a=1.
ü PROPIEDAD CÍCLICA (O CIRCULAR) MODIFICADA:
Pa/bPb/c=Pa/c`Pa/bPb/cPc/d=Pa/d`etc.
Desde un punto de vista teórico es deseable que los números índices para grupos de artículos tengan las propiedades que cumplían las relaciones (números índices para un solo artículo). Todo número índice que tenga tal o cual propiedad se dice que satisface el criterio asociado con ella. Por ejemplo, los números índices que tengan la propiedad de inversión temporal se dirá que satisface el criterio de inversión temporal, etc.
No se conoce ningún número índice que cumpla todos los criterios, si bien en muchos casos se satisfacen aproximadamente. El índice ideal de Fisher, que en particular verifica el criterio de inversión temporal y el de inversión de factores, es mejor que cualquier otro número índice útil en cuanto a satisfacer las propiedades consideradas importantes ( de ahí el apelativo de ideal).
Desde una perspectiva práctica, no obstante, otros números índices sirven también, y examinaremos algunos de ellos.
Cuando se determina un Índice en la mayoría de los casos se trata de obtenerlo en un grupo homogéneo de artículos y no en uno en particular. No sería conveniente hacer una lista con todos esos precios, lo ideal sería disponer de un solo número índice de precios compare los precios en varios períodos.
Por ejemplo; al calcular un índice de precios al consumo debemos decidir que artículos o servicios deben incluirse, así como su peso de importancia, datos referentes a precios y cantidades de los artículos, calidades de los artículos; en fin obtener un solo índice del coste de la vida que tenga significado práctico.
En la práctica es deseable que el período base elegido para la comparación sea un período de estabilidad económico no muy alejado en el pasado. De cuando en cuando puede ser necesario, por tanto, cambiar el período base.
Una posibilidad es recalcular todos los números índice en términos del nuevo período base. Un método aproximado más simple consiste en dividir todos los números índice para los diversos años correspondientes al período base antiguo por los números índice para los diversos años correspondientes al nuevo período base, expresando los resultados como porcentajes. Estos resultados representan los nuevos números índice, siendo el número índice para el nuevo período base 100 (%), como debe ser.
Matemáticamente hablando, este método es estrictamente aplicable solo si los números índices satisfacen el criterio circular. Sin embargo, para muchos tipos de índices el método, afortunadamente, da resultados que en la práctica son suficientemente próximos a los que se tendrían teóricamente.
Aunque los ingresos de las personas puedan estar creciendo teóricamente durante un cierto número de años, sus ingresos reales pueden en verdad estar disminuyendo debido al aumento del coste de la vida, en tanto en cuanto este aumento del coste de la vida hace que disminuya su poder adquisitivo. Calculamos los ingresos reales dividiendo los ingresos aparentes de cada año por el número índice del coste de la vida en ese año, usando un período base adecuado. Por ejemplo, si los ingresos de un individuo en 1980 son de 150% de sus de 1970 (o sea han crecido en 50%) y el coste de la vida se ha doblado en ese mismo período de tiempo, entonces sus ingresos reales en 1980 son sólo del 150/2 = 75% de lo que eran en 1970.
En términos matemáticos, éste método de deflación de series en el tiempo es estrictamente aplicable sólo si los números índice cumplen el criterio de inversión de factores, y por esta razón el índice ideal de Fisher es adecuado. No obstante, otros números índice dan también resultados correctos a efectos prácticos.
Los índices de Paasche y Laspeyres son utilizados frecuentemente para el cálculo del Índice de precios de cantidades, por lo general ofrecen diferentes resultados, esto se debe a la diferencia en los pesos. No se puede decir que fórmula es precisa o mejor; cada una de ella es significativa ya que tiene una interpretación física simple. Si, por ejemplo, el índice de precios calculado por un método es 110 y por otro método es 130, podemos decir entonces que el nivel de precios ha cambiado de 100 a entre 110 y 130.
Las principales ventajas de este índice de pesos fijos más general son que evita la predisposición parcial hacia los precios, inherentes a los ya mencionados índices de Laspeyres y Paasche, y permite una comparación directa de los movimientos de los precios de un período con la base.
ü MÉTODO DE AGREGACIÓN SIMPLE: Expresa el precio de los artículos en el año dado como porcentaje del precio total de los artículos en año base.
∑ P0 = suma de todos los precios de los artículos en el año base.
∑ Pn = suma de todos los precios de los artículos en el año dado
Y donde el resultado se expresa con porcentaje, al igual que se hace con los números índices en general.
Aunque este método es fácil de aplicar, tiene dos grandes desventajas que lo convierten en insatisfactorio:
a) No tiene en cuenta la importancia relativa de los diversos artículos. Así pues, asigna igual peso a la leche que a la crema de afeitar a la hora de calcular el índice de precios al consumo.
b) Las unidades escogidas al anotar los precios (galones, bushels, libras...) afectan al índice.
a) ÍNDICE DE LASPEYRES O MÉTODO DEL AÑO BASE:
b) ÍNDICE DE PAASCHE O MÉTODO DEL AÑO DADO:
c) EL MÉTODO DEL AÑO TÍPICO:
Si q denota la cantidad durante algún período típico t, definimos Índice de Precios por agregación ponderada con pesos de cantidad en el año típico
Para t = 0 y t = n, esto se reduce a las ecuaciones de Laspeyres y Paasche respectivamente.
ü ÍNDICE IDEAL DE FISHER: Este índice de precios es la media geométrica de los números índices de Laspeyres y de Paasche. El índice ideal de Fisher satisface los criterios de inversión temporal y de inversión de factores, lo que confiere una cierta ventaja teórica sobre otros números índice.
ü EL ÍNDICE DE MARSHALL-EDGEWORTH: El índice de Marshall-Edgeworth usa el método de agregación ponderada con año típico, en el que los pesos se toman como la media aritmética de las cantidades del año base y del año dado; Es decir, q1= ½ (qo + qn). Sustituyendo este valor de q en la ecuación (8) resulta:
ü EL MÉTODO DEL PROMEDIO PONDERADO DE RELACIONES: Para paliar las ventajas del método del promedio simple de relaciones se puede usar un promedio ponderado de relaciones. El promedio ponderado más utilizado es la media aritmética ponderada, aunque también se utilizan otros, como la media geométrica ponderada.
En este método asignamos a cada relación de precios un peso dado por el valor total del artículo en términos de alguna unidad monetaria, digamos el dólar. Como el valor de un artículo se obtiene multiplicando su precio p por la cantidad q, los pesos vienen dados por pq.
Según se use el año base, el año dado o el año típico para calcular tales pesos (denotados respectivamente por p0qo, pnqn, y p1q1), usamos una u otra de las fórmulas siguientes:
Media aritmética ponderada de relaciones de precios, usando pesos del año base:
Media aritmética ponderada de relaciones, usando pesos de un año típico:
Media aritmética ponderada de relaciones de precios, usando pesos de un año típico:
ü NÚMEROS ÍNDICE DE CANTIDAD O VOLUMEN:
Índice de media aritmética simple de relaciones de volumen =
Donde ∑ qn / q0 = suma de relaciones de cantidad de todos los artículos.
N = número de relaciones de cantidad usadas
ü NÚMEROS ÍNDICES DE VALOR:
Donde:
∑p0 q0 = valor total de todos los artículos en el período base.
∑pn qn = valor total de todos los artículos en el periodo dado.
ü MÉTODO DEL PROMEDIO SIMPLE DE RELACIONES: El índice producido por éste método depende del procedimiento utilizado para promediar las relaciones de precios; los procedimientos incluyen media aritmética, la geométrica, la armónica y la mediana. Con la media aritmética, por ejemplo, tendríamos:
Índice de la media aritmética simple de relaciones de precios
Donde:
∑ Pn / P0 = suma de todas las relaciones de precios de los artículos.
N = Número de relaciones de precios de artículos utilizados.
Si bien este método no tiene la segunda desventaja antes citada, todavía mantiene la primera.
ü MÉTODO DE AGREGACÓN PONDERADA: Con el fin de evitar las desventajas del método de agregación simple, asignamos un peso al precio de cada artículo, en general la cantidad (o volumen) vendida durante el año dado o un año típico (que pude ser un promedio de varios años). Tales pesos indican la importancia del artículo en cuestión. Dependiendo de que se use el año base, el año dado o un año típico denotados respectivamente por qo, qn, y qt, usamos una de las siguientes fórmulas:
Se puede notar que los números índices son útiles para los economistas, pronosticadores, estadísticos y encargados de tomar decisiones en los negocios que estudian la magnitud y la dirección de los movimientos en la economía.
Por lo tanto los números índices son una especie de barómetros de cambios en los negocios, también son importantes para pronosticar la actividad económica futura
Con frecuencia se usan en análisis de series de tiempo, el estudio histórico de las tendencias y las variaciones que pueda tener una economía; todo esto con el fin de que los dirigentes de negocios e incluso de países puedan mantenerse al mismo ritmo con las cambiantes condiciones económicas y de esta manera contar con una mejor información para una buena toma de decisiones.