UNA MIRADA A LAS MEDIDAS DE POSICIÓN ESTADÍSTICA

ESCUELA SUPERIOR DE ADMINISTRACIÓN PÚBLICA ESAP

ACTIVIDAD PARA ESTUDIANTES DE  III. SEMESTRE DE APT

TERRITORIAL CAUCA

Profesor: Fabián Orozco Méndez

Tutor.

CUARTILES, DECILES Y PERCENTILES

Las medidas de posición dividen un conjunto de datos en grupos con el mismo número de individuos.

Para calcular las medidas de posición es necesario que los datos estén ordenados de menor a mayor.

La medidas de posición son:

Cuartiles

Los cuartiles son los tres valores de la variable que dividen a un conjunto de datos ordenados en cuatro partes iguales.

Q₁, Q₂ y Q₃ determinan los valores correspondientes al 25%, al 50% y al 75% de los datos.

Q₂ coincide con la mediana.

Cálculo de los cuartiles

1 Ordenamos los datos de menor a mayor.

2 Buscamos el lugar que ocupa cada cuartil mediante la expresión .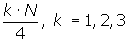

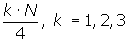Número impar de datos

2, 5, 3, 6, 7, 4, 9

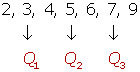
Número par de datos

2, 5, 3, 4, 6, 7, 1, 9

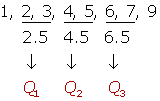
Cálculo de los cuartiles para datos agrupados

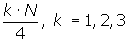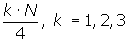En primer lugar buscamos la clase donde se encuentra , en la tabla de las frecuencias acumuladas.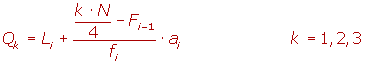

L_i es el límite inferior de la clase donde se encuentra la mediana.

N es la suma de las frecuencias absolutas.

F_i-1 es la frecuencia acumulada anterior a la clase mediana.

a_i es la amplitud de la clase.

Ejercicio de cuartiles

Calcular los cuartiles de la distribución de la tabla:

	fi	Fi
[50, 60)	8	8
[60, 70)	10	18
[70, 80)	16	34
[80, 90)	14	48
[90, 100)	10	58
[100, 110)	5	63
[110, 120)	2	65
	65

Cálculo del primer cuartil

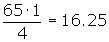
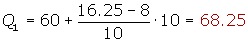
Cálculo del segundo cuartil

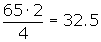
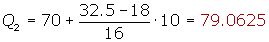
Cálculo del tercer cuartil

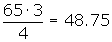
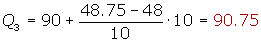
Deciles

Los deciles son los nueve valores que dividen la serie de datos en diez partes iguales.

Los deciles dan los valores correspondientes al 10%, al 20%... y al 90% de los datos.

D₅ coincide con la mediana.

Cálculo de los deciles

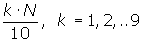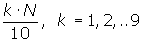En primer lugar buscamos la clase donde se encuentra , en la tabla de las frecuencias acumuladas.

L_i es el límite inferior de la clase donde se encuentra la mediana.

N es la suma de las frecuencias absolutas.

F_i-1 es la frecuencia acumulada anterior a la clase mediana.

a_i es la amplitud de la clase.

Ejercicio de deciles

Calcular los deciles de la distribución de la tabla:

	fi	Fi
[50, 60)	8	8
[60, 70)	10	18
[70, 80)	16	34
[80, 90)	14	48
[90, 100)	10	58
[100, 110)	5	63
[110, 120)	2	65
	65

Cálculo del primer decil

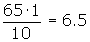
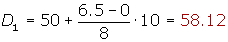
Cálculo del segundo decil

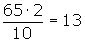
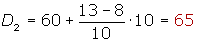
Cálculo del tercer decil

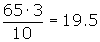
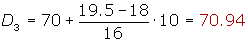
Cálculo del cuarto decil

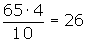
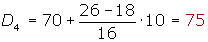
Cálculo del quinto decil

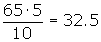
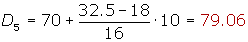
Cálculo del sexto decil

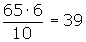
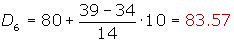
Cálculo del séptimo decil

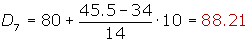
Cálculo del octavo decil

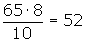
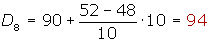
Cálculo del noveno decil

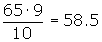
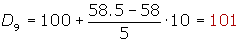
Percentiles

Los percentiles son los 99 valores que dividen la serie de datos en 100 partes iguales.

Los percentiles dan los valores correspondientes al 1%, al 2%... y al 99% de los datos.

P₅₀ coincide con la mediana.

Cálculo de los percentiles

En primer lugar buscamos la clase donde se encuentra , en la tabla de las frecuencias acumuladas.

L_i es el límite inferior de la clase donde se encuentra la mediana.

N es la suma de las frecuencias absolutas.

F_i-1 es la frecuencia acumulada anterior a la clase mediana.

a_i es la amplitud de la clase.

Ejercicio de percentiles

Calcular el percentil 35 y 60 de la distribución de la tabla:

	fi	Fi
[50, 60)	8	8
[60, 70)	10	18
[70, 80)	16	34
[80, 90)	14	48
[90, 100)	10	58
[100, 110)	5	63
[110, 120)	2	65
	65

Percentil 35

Percentil 60